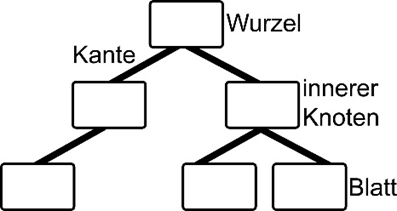Ein Binärbaum ist eine hirarische Datenstruktur. Das bedeutet, dass er nicht linear ist und damit nicht die Objekte in einer einfachen Reihenfolge darstellt. Baumstruktur Ein Baum besteht aus Knoten, die mit Kanten verbunden werden. Dabei kann man ihn abstrakt als Wurzel beschreiben, die eine linkes und ein rechtes kind hat. Dieses Kind kann eine weitere Wurzel sein(global betrachtet dann innerer Knoten gennant) oder aber ein Blatt sein, also keine weiteren Kinder haben. Jeder knoten hat ein Element der zu speichernden Daten. 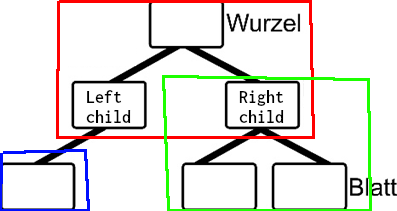Baumstruktur Die Rot-markierten knoten stellen eine Baum dar, ebenso wie die grün markierten. Dies Zeigt, wie ein innerer Knoten(der rechte rote) zur Wurzel des Grünen Baums wird/ist.

Der geordnete Binärbaum

In einem geordneten Binärbaum, sind die daten geordnet vorliegend. Dabei ist der Inhalt jedes linken Teilbaums kleiner, als der der Wurzel und der Inhalt jedes rechten Teilbaums größer als die Wurzel. Ein Beispiel dafür wäre das folgende.

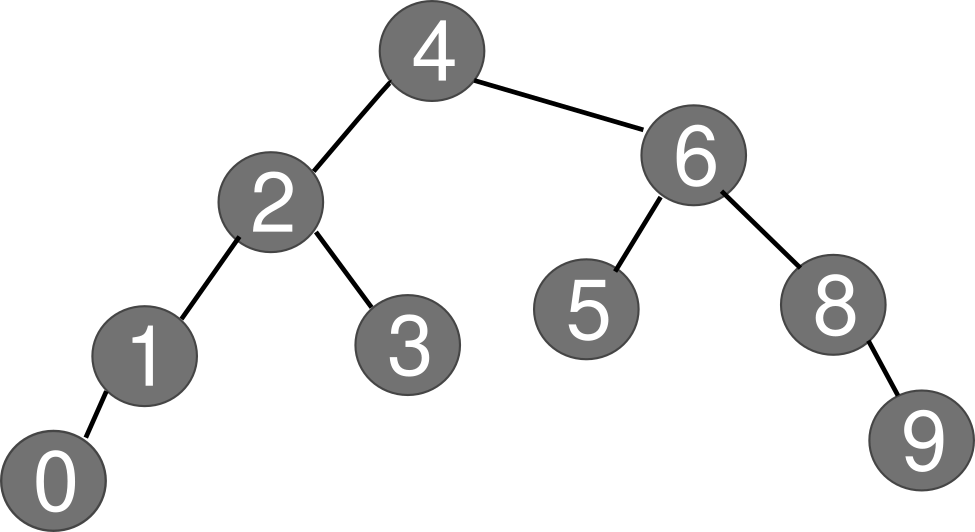
Baumstruktur

Man nennt ihn auch BinarySearchTree.

Die Java-Klasse dazu kann folgendermaßen aussehen.

classDiagram class TreeContent { content Content leftchild : Tree rightchild : Tree

}

Die wichtigen Methoden hierbei sind Daten einzufügen, zu entfernen und abzurufen. Diese werden folgendermaßen implementiert:

Suchen

    public ContentType search(ContentType pContent) {
        // Wenn wir kein element haben, dann abbrechen
        if (this.isEmpty() || pContent == null) {
            return null;
        } else {
            ContentType content = this.getContent();
            if (pContent.isLess(content)) {
                // Das gesuche element ist kleiner, also suchen wir im linken Teilbaum
                return this.getLeftTree().search(pContent);
            } else if (pContent.isGreater(content)) {
                // Das gesuche element ist größer, also suchen wir im rechten Teilbaum
                return this.getRightTree().search(pContent);
            } else if (pContent.isEqual(content)) {
                // Element wurde gefunden.
                return content;
            } else {
                // Wir haben das element nicht gefunden
                return null;
            }
        }
    }

Einfügen

Da in BinarySearchTrees alle Objekte eindeutig sind, doppeln sich Objekte niemals und können daher beim einfügen ignoriert werden.

    public void insert(ContentType pContent) {
        // Wir fügen nichts leeres ein.
        if (pContent != null) {
            if (isEmpty()) {
                //Wenn der aktuelle Baum leer ist, dann erzeugen wir eine neue Node
                this.node = new BSTNode<ContentType>(pContent);
            } else if (pContent.isLess(this.node.content)) {
                // Wir versuchen das objekt in the linken seite einzufügen
                this.node.left.insert(pContent);
            } else if(pContent.isGreater(this.node.content)) {
                // Wir versuchen das objekt in the rechten seite einzufügen
                this.node.right.insert(pContent);
            }
        }
    }

Entfernen

    public void remove(ContentType pContent) {
    // Wenn der Baum leer ist, dann abbrechen
    if (isEmpty() || pContent == null ) {
        return;
    }
    // Zu löschendes Element ist kleiner als aktuelles, daher suchen wir im linken Teilbaum
    if (pContent.isLess(node.content)) {
        node.left.remove(pContent);
    // Wenn es größer ist, dann muss es im rechten gelöscht werden.
    } else if (pContent.isGreater(node.content)) {
        node.right.remove(pContent);
    // Das element ist gefunden und soll hier gelöscht werden
    } else {
    // Wenn wir kein linkes blatt haben
    if (node.left.isEmpty()) {
        // Wenn der Knoten ein Blatt ist und keine Nachfolger hat einfach auf null setzten.
        if (node.right.isEmpty()) {
            node = null;
        // Wir haben nur einen rechten nachfolger
        } else {
            node = getNodeOfRightSuccessor();
        }
        // Wir haben nur einen linken nachfolger
        } else if (node.right.isEmpty()) {
            node = getNodeOfLeftSuccessor();
        } else {
            // Es gibt links und rechts einen Nachfolger.
            if (getNodeOfRightSuccessor().left.isEmpty()) {
                // Der rechte Nachfolger hat keinen linken Nachfolger.
                node.content = getNodeOfRightSuccessor().content;
                node.right = getNodeOfRightSuccessor().right;
            } else {
                BinarySearchTree<ContentType> previous = node.right.ancestorOfSmallRight();
                BinarySearchTree<ContentType> smallest = previous.node.left;
                this.node.content = smallest.node.content;
                previous.remove(smallest.node.content);
            }
        }
    }
}