Sortierverfahren
Selection Sort
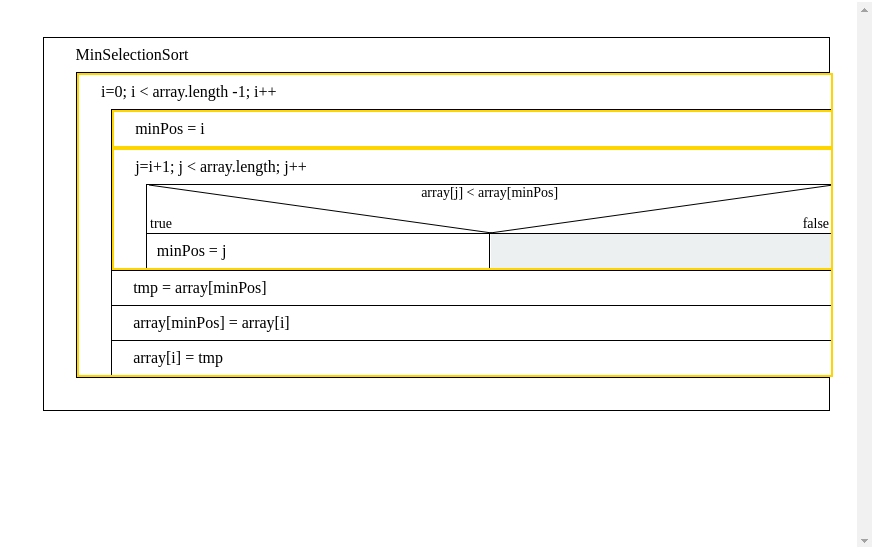
Es gibt das min und das max selection sort verfahren. Beim Min-Selection sort wird immer aus einem unsortierten bereich das minimum herausgesucht und dann als letztes Element der sortierten Menge angefügt.
Struktogram
Java Implementierung
public static void minSort(int[] a) { for (int iUnsorted = 0; iUnsorted < a.length-1; iUnsorted++) { int minPos = iUnsorted; // Den index vom kleinsten wert in der unsortierten Menge finden. for (int j=iUnsorted+1; j<a.length; j++) { if(a[j] < a[minPos]) { minPos = j; } } // Den kleinsten wert and den niedrigsten Index der unsortierten Menge setzen int tmp = a[iUnsorted]; a[iUnsorted] = a[minPos]; a[minPos] = tmp; } }
Merge Sort
Funktionsweise
Die liste wird immer weiter in kleinere listen unterteilt, bis diese die länge 1 haben, also praktisch sortiert sind. Dann werden diese wieder sortiert zusammengeführt, daher der name merge sort(engl. merge sortieren) Dies ist nicht nur von der Komplexität sehr effektiv (O(log n)), sondern ist durch die vielen kleinen prozesse gut auf meherere Prozesse Skallierbar.
Programablaufplan
result, left, right| B[leftindex = 0
rightindex = 0
resultindex = 0] B --> C[ ] C --> D{resultindex < result.length} D --> |False| E([End]) D --> |True| F{leftindex >= left.length} G --> C F --> |False| H{rightindex >= right.length} H --> |False| I{"left[leftindex] < right[rightindex]"} F --> |True| G["result[resultIndex] = right[rightindex];
rightindex++;
resultIndex++;"] I --> |False| G I --> |True| J["result[resultindex] = left[leftindex];
leftindex++;
resultindex++;"] J --> C
Java Implementierung
public static void mergeSort(int[] a, int n) { if (n < 2) { return; } int mid = n / 2; int[] l = new int[mid]; int[] r = new int[n - mid]; for (int i = 0; i < mid; i++) { l[i] = a[i]; } for (int i = mid; i < n; i++) { r[i - mid] = a[i]; } mergeSort(l, mid); mergeSort(r, n - mid); merge(a, l, r, mid, n - mid); } // Bringt zwei sortierte arrays in ein grosses array zusammen public static void merge(int[] a, int[] l, int[] r, int left, int right) { int i = 0, j = 0, k = 0; while (i < left && j < right) { if (l[i] <= r[j]) { a[k++] = l[i++]; } else { a[k++] = r[j++]; } } while (i < left) { a[k++] = l[i++]; } while (j < right) { a[k++] = r[j++]; } }
Quick sort
Funktionsweise
Beim quicksort gibt es einen Pivot Point Um den herum sortiert werden. Alle werte kleiner, als der Pivot werden links davon eingeordnet, und alle größer, rechts davon. Dazu werden eine rechte und eine linke schranke definiert, die immer weiter richtung Pivot gehen. Wenn das Element an unserer linken Marke nun einen größeren Wert, als Pivot hat und die Linke Marke einen größeren, dann werden diese beiden vertauscht.
Programablaufplan
left=0
right=n-1"] A --> B{left < right} B --> |True| C{"a[right] >= pivot"} B --> |False| K["a[left] = pivot"] K --> Y([End]) C --> |True| D["right += 1"] D --> E{left != right} C --> |False| E E --> |True| F["a[left] = a[right]
left += 1"] F --> G{"a[left] < pivot"} E --> |False| G G --> |True| H[left += 1] H --> I{left != right} G --> |False| I I --> |False| B I --> |True| J["a[right] = a[left]
right -= 1"] J --> B
Java implementierung
Implementiert wird der Quick sort wieder in rekursiver form
public static void quicksort(int[] a, int lo, int hi) { //Wenn unser array nur noch ein element hat, ist es sortiert if(lo>=hi) return; //Pivot element als mittleres element bestimmen int pivot = a[lo+(hi-lo)/2]; //Rechte und linke marken erstellen int r = hi; int l = lo; while(l>r) { // Wert, der nach rechts muss finden while (a[l] < pivot) l++; // Wert, der nach links muss finden while (a[r] > linke) r --; if( a[r] == a[l]) { r--; } else { //Werte vertauschen int tmp = a[r]; a[r] = a[l]; a[l] = tmp; } } /* Rekursiver aufruf Am ende ist der index des pivot elements = l = r, daher kann man sich aussuchen, welchen index man nimmt. Ich nehme l. */ quicksort(a, lo, l-1); quicksort(a, l+1, hi); }
Insertion Sort
Funktionsweise
Beim insertion sort gibt es einen sortierten und einen unsortierten bereich. Man kann sich hierbei aussuchen, ob man diesen Bereich oben, also für die großen Zahlen, oder unter für die kleinen Zahlen haben möchte. Der sortierte Bereich ist anfangs 1 element groß. Ich erklähre hier das sortieren mit dem kleineren sortierten Bereich. Es wird immer das erste Element der unsortierten bereichs mit dem letzten der sortierten verglichen. Ist das unsortierte Element kleiner, wird es mit dem vorletzten Element verglichen, bis es größer ist. Dann wird es nach dem kleinen Element eingefügt, daher auch der Name. So wird der sortierte Bereich um 1 größer, und das neue erste Element der unsortierten Bereichs wird verglichen. Dies passiert, bis der unsortierte Bereicht leer ist, und damit das ganze Array sortiert ist.
Java Implementierung
Man kann den Insertion Sort sowohl rekursiv, als auch iterativ implementieren. Beim Aufruf der Rekursiven Implementierung, muss man als zweites Parameter den index=0 angeben.
public static void insertion_sort_rekursiv(int[] a, int index) { if(a[index] >= a[index-1]) { int tmp = a[index]; a[index] = a[index-1]; a[index-1] = tmp; } else { insertion_sort_rekursiv(a, index+1); } } public static void insertion_sort(int[] a) { for (int i=1; i<a.length; i++) { int tmp = a[i]; int j; for(j=i-1; j>=0; j--) { if(a[j] > tmp) { a[j+1] = a[j]; } else break; } a[j+1] = tmp; } }