Ansatz
Im Grunde genommen ist das Vigénere-Verfahren eine Erweiterung von Cäsar. Dabei Verschlüsseln wir nicht mit einem konstanten offset, wie bei Cäsar, sondern mit einem Schlüsselwort. Dabei wird dann das Schlüsselwort so lange hintereinandergeschrieben, bis es die Länge des zu verschlüsselnden textes erreicht. Dann wird dabei der Index des Schlüssel-Buchstaben, an der entsprechenden Stelle jedes Klartextbuchstaben zur Cäsarverschlüsselung benutzt. Da nun nicht mehr der gesammte Text mit einer einzigen Verschiebung verschlüsselt wird, funktioniert hierbei, solange die Schlüsselwortlänge nicht 1 ist, eine normale Häufigkeitsanalyse nicht mehr. Genau wie bei Cäsar ist hier die Verschlüsselung die gleiche Methodik, wie die Entschlüsselung, abgesehen von der entegengesetzte Richtung bei der Verschiebung
| Text | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Schlüssel | H | A | L | L | O | H | A | L | L | O |
| Klartext | I | N | F | O | R | M | A | T | I | K |
| Ciffertext | P | N | Q | Z | F | T | A | E | T | Y |
public static String Vverschluesseln(String pKlartext, String pSchluesselwort) { pSchluesselwort = pSchluesselwort.toUpperCase(); String res = ""; int key_index = 0; for(int i=0; i<pKlartext.length(); i++) { if(key_index == pSchluesselwort.length()) key_index = 0; char v = 'A'; v = pKlartext.charAt(i); if((v < 'A' || v > 'Z') && (v < 'a' || v > 'z')) { res += v; } else { int p = v >= 'a' ? v - 'a' : v - 'A'; int k = pSchluesselwort.charAt(key_index) - 'A'; p = (p + k) % 26; char a = v >= 'a' ? (char) (p + 'a') : (char) (p + 'A'); res += a; key_index++; } } return res; }
Knacken
Wie oben schon angesprochen kann man Vigenere nicht mehr über eine einfache Häufigkeitsanalyse knacken. Jedoch lässt sich eine Häufigkeitsanalyse durchführen, wenn man die Länge des Schlüssels besitzt. Denn dann kann man eine Häufigkeitsanalyse auf jeden Buchstaben des Schlüssels anwenden und dadurch den jeweiligen Versatz herausfinden. Deshalb ist auch ein Bruteforcen durch längere Schlüssel immer weniger effizient.
Kasiski-Test
Der erste Ansatz die Schlüsselwortlänge zu bestimmen ist der s.g. Kasiski Test. Dabei versuchen wir Glück zu haben und gleiche Schlüsselwortbuchstaben auf gleiche Klartextbuchstabenfolgen mehrmals treffen zu lassen. Als Beispiel kann man sich das vorstellen, dass z.B. das Wort Die relativ häufig in einem Satz vorkommt. Daher gibt es eine warscheinlichkeit, dass an mehreren Stellen z.B. das hal aus dem Schlüssel Hallo genau dieses Wort veschlüsselt. Dies sehen wir dann anhand von Mustern im Ciffertext. Daher ist Vigenere bei kürzeren Schlüsseln relativ unsicher.
EYRYCFWL JHFHSIUB HMJOUCSE GTNEERFL JLVSXMVY SSTKCMIK ZSJHZVBF XMXKPMMV WOZSIAFC RVFTNERH MCGYSOVY VFPNEVHJ AOVWUVYJ UFOISHXO VUSFMKRP TWLCIFMW VZTYOISU UIISECIZ VZVYVFPC QUCHYRGO MUWKVBNX VBVHHWIF LMYFFNEV HJAOVWUL YERAYLER VEEKSOCQ DCOUXSSL UQVBFMAL FEYHRTVY VXSTIVXH EUWJGJYA RSILIERJ BVVFBLFV WUHMTVUA IJHPYVKK VLHVBTCI UISZXVBJ BVVPVYVF GBVIIOVW LEWDBXMS SFEJGFHF VJPLWZSF CRVUFMXV ZMNIRIGA ESSHYPFS TNLEHUYR
Wenn man sich nun Muster heraussucht und deren Abstände misst, so kann man diese Abstände per Primfaktorzerlegung zerlegen. Und diese Faktoren geben einem Rückschlüsse auf die schlüssellänge.
| Folge | Abstand | Primfaktoren |
|---|---|---|
| TNE | 50 | 2 * 2 * 5 |
| FCRV | 275 | 7 * 5 * 5 |
| NEVHJAOVWU | 180 | 3 * 3 * 2 * 2 * 5 |
| VWU | 165 | 3 * 5 * 11 |
| OIS | 25 | 5 * 5 |
Da wir als Primfaktoren nun eine extrem hohe Anzahl an fünfen finden können wir als Resultat des Kasiski-Testes Fünf als Potenzielle Schlüssellänge ansehen. Dies ist aber keine Garantie.
Friedman-Test
Der Friedman-Test nimmt einen Mathematischen Ansatz auf Basis der Warscheinlichkeiten, dass ein zufälligges Buchstabenpaar aus dem Klartext aus den gleichen Buchstaben besteht.
Wenn unser Text aus einer komplett zufälligen Buchstabenfolge besteht ist die Anzahl der gleichen Paare


I_d = 0.0762.
Als Angreifer berechnen wir nun den Index I für unseren Text.
Je länger das Schlüsselwort wird, desto geringer ist diese Warscheinlichkeit von Mustern.
Daher wird dabei unser I immer kleiner.
Daraus lässt sich die Formel für die Schlüsselwortlänge h herleiten.

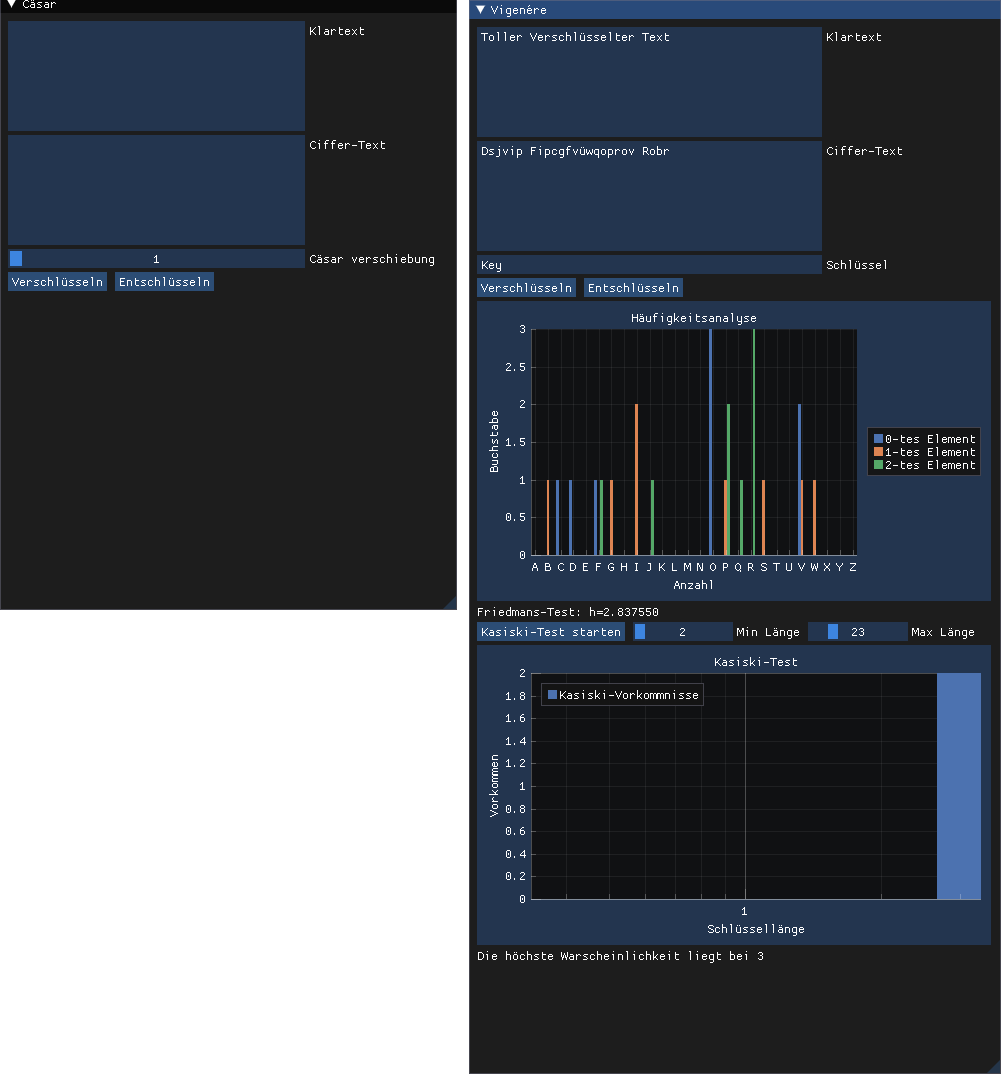
Meine Eigene Lösung
Ich habe eine recht coole eigene C++ Applikation unter dem Namen DJ-Crypt geschrieben, um den Kasiski und Friedman Test fast automatisch durchzuführen.
Es bietet mehrere Werkzeuge, um die Schlüssellänge und über Häufigkeitsanalyse auch den Schlüssel zu finden.